Stability is more complex and in some manifestations more difficult to measure than strength and stiffness but can be broadly defined as capacity to resist:
• Displacement
• Overturning
• Collapse
• Buckling
Diagrams 1-3 give a theoretical definition; all the other diagrams illustrate stability of conceptual structures.
1 Unstable
2 Neutral
3 Stable
4 Weak stability: high center of gravity, narrow base
5 Strong stability: low center of gravity, broad base
6 Unstable post and beam portal
7 Stable moment frame
8 Unstable T-frame with pin joint at base
9 Stable twin T-frames
Buckling stability
Buckling stability is more complex to measure than strength and stiffness and largely based on empirical test data.. This introduction of buckling stability is intended to give only a qualitative intuitive understanding.
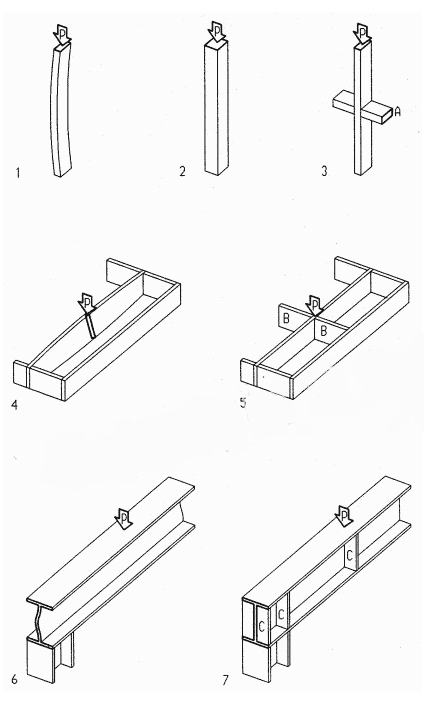
Column buckling is defined as function of slenderness and beam buckling as function of compactness. A formula for column buckling was first defined in the 18th century by Swiss mathematician Leonhard Euler. Today column buckling is largely based on empirical tests which confirmed Euler’s theory for slender columns; though short and stubby columns may crush due to lack of compressive strength.
Beam buckling is based on empirical test defined by compactness, a quality similar to column slenderness.
1 Slender column buckles in direction of least dimension
2 Square column resist buckling equally in both directions
3 Blocking resists buckling about least dimension
4 Long and slender wood joist subject to buckling
5 blocking resists buckling of wood joist
6 Web buckling of steel beam
7 Stiffener plates resist web buckling
A Blocking of wood stud
B Blocking of wood joist
C Stiffener plate welded to web
P Load
• Displacement
• Overturning
• Collapse
• Buckling
Diagrams 1-3 give a theoretical definition; all the other diagrams illustrate stability of conceptual structures.
1 Unstable
2 Neutral
3 Stable
4 Weak stability: high center of gravity, narrow base
5 Strong stability: low center of gravity, broad base
6 Unstable post and beam portal
7 Stable moment frame
8 Unstable T-frame with pin joint at base
9 Stable twin T-frames
Buckling stability
Buckling stability is more complex to measure than strength and stiffness and largely based on empirical test data.. This introduction of buckling stability is intended to give only a qualitative intuitive understanding.
Column buckling is defined as function of slenderness and beam buckling as function of compactness. A formula for column buckling was first defined in the 18th century by Swiss mathematician Leonhard Euler. Today column buckling is largely based on empirical tests which confirmed Euler’s theory for slender columns; though short and stubby columns may crush due to lack of compressive strength.
Beam buckling is based on empirical test defined by compactness, a quality similar to column slenderness.
1 Slender column buckles in direction of least dimension
2 Square column resist buckling equally in both directions
3 Blocking resists buckling about least dimension
4 Long and slender wood joist subject to buckling
5 blocking resists buckling of wood joist
6 Web buckling of steel beam
7 Stiffener plates resist web buckling
A Blocking of wood stud
B Blocking of wood joist
C Stiffener plate welded to web
P Load