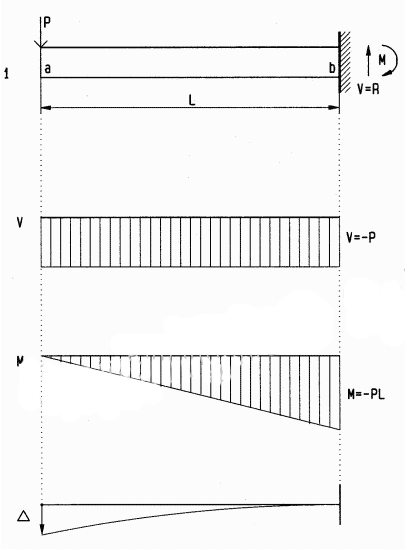
Cantilever beam with point load
Assume a beam of length L = 10 ft, supporting a load P = 2 k. The beam bending moment and shear force may be computed, like the external reactions, by equations of equilibrium ΣH=0, ΣV= 0, and ΣM=0. Bending moment and shear force cause bending-and shear stress, similar to axial load yielding axial stress f= P/A.
1 Cantilever beam with concentrated load
V Shear diagram (shear force at any point along beam)
M Bending moment diagram (bending moment at any point along beam)
∆ Deflection diagram (exaggerated for clarity)
Reactions, found by equilibrium, ΣV=0 (up +) and ΣM=0 (clockwise +)
Shear V, found by vertical equilibrium, ΣV=0 (up +)
Left of a and right of b, shear is zero because there is no beam to resist it (reaction at b reduces shear to zero). Shear may be checked, considering it starts and stops with zero. Concentrated loads or reactions change shear from left to right of them. Without load between a and b (beam DL assumed negligible) shear is constant.
Bending moment M, found by moment equilibrium, ΣM=0 (clockwise +)
The mid-span moment being half the moment at b implies linear distribution. The support reaction moment is equal and opposite to the beam moment.
Deflection ∆ is described later. Diagrams visualize positive and negative bending by concave and convex curvature, respectively. They are drawn, visualizing a highly flexible beam, and may be used to verify bending.
Assume a beam of length L = 10 ft, supporting a load P = 2 k. The beam bending moment and shear force may be computed, like the external reactions, by equations of equilibrium ΣH=0, ΣV= 0, and ΣM=0. Bending moment and shear force cause bending-and shear stress, similar to axial load yielding axial stress f= P/A.
1 Cantilever beam with concentrated load
V Shear diagram (shear force at any point along beam)
M Bending moment diagram (bending moment at any point along beam)
∆ Deflection diagram (exaggerated for clarity)
Reactions, found by equilibrium, ΣV=0 (up +) and ΣM=0 (clockwise +)
Shear V, found by vertical equilibrium, ΣV=0 (up +)
Left of a and right of b, shear is zero because there is no beam to resist it (reaction at b reduces shear to zero). Shear may be checked, considering it starts and stops with zero. Concentrated loads or reactions change shear from left to right of them. Without load between a and b (beam DL assumed negligible) shear is constant.
Bending moment M, found by moment equilibrium, ΣM=0 (clockwise +)
The mid-span moment being half the moment at b implies linear distribution. The support reaction moment is equal and opposite to the beam moment.
Deflection ∆ is described later. Diagrams visualize positive and negative bending by concave and convex curvature, respectively. They are drawn, visualizing a highly flexible beam, and may be used to verify bending.