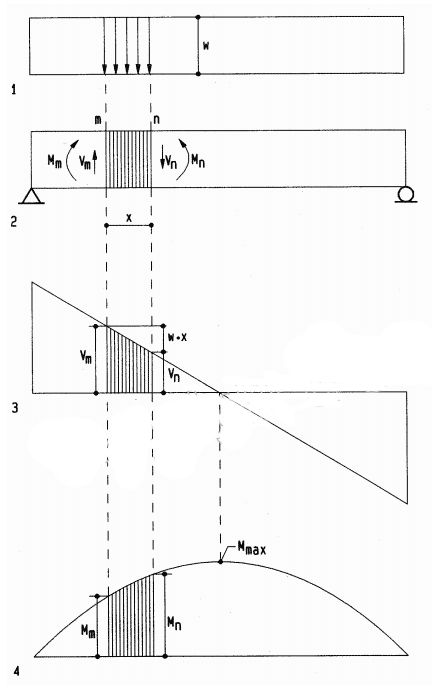
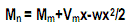The area method for beam design simplifies computation of shear forces and bending moments and is derived, referring to the following diagrams:
1 Load diagram on beam
2 Beam diagram
3 Shear diagram
4 Bending diagram
The area method may be stated:
• The shear at any point n is equal to the shear at point m plus the area of the load diagram between m and n.
• The bending moment at any point n is equal to the moment at point m plus the area of the shear diagram between m and n.
The shear force is derived using vertical equilibrium:
∑ V = 0; Vm - w x - Vn = 0; solving for Vn
Vn = Vm-wx
where w x is the load area between m and n (downward load w = negative).
The bending moment is derived using moment equilibrium:
∑ M = 0; Mm + Vmx – w x x/2 - Mn = 0; solving for Mn
where Vmx – wx^2/2 is the shear area between m and n, namely, the rectangle Vm x less the triangle w x^2/2. This relationship may also be stated as Mn = Mm + Vx, where V is the average shear between m and n.
By the area method moments are usually equal to the area of one or more rectangles and/or triangles. It is best to first compute and draw the shear diagram and then compute the moments as the area of the shear diagram.
From the diagrams and derivation we may conclude:
• Positive shear implies increasing bending moment.
• Zero shear (change from + to -) implies peak bending moment (useful to locate maximum bending moment).
• Negative shear implies decreasing bending moment. Even though the forgoing is for uniform load, it applies to concentrated load and non-uniform load as well. The derivation for such loads is similar.
1 Load diagram on beam
2 Beam diagram
3 Shear diagram
4 Bending diagram
The area method may be stated:
• The shear at any point n is equal to the shear at point m plus the area of the load diagram between m and n.
• The bending moment at any point n is equal to the moment at point m plus the area of the shear diagram between m and n.
The shear force is derived using vertical equilibrium:
∑ V = 0; Vm - w x - Vn = 0; solving for Vn
Vn = Vm-wx
where w x is the load area between m and n (downward load w = negative).
The bending moment is derived using moment equilibrium:
∑ M = 0; Mm + Vmx – w x x/2 - Mn = 0; solving for Mn
where Vmx – wx^2/2 is the shear area between m and n, namely, the rectangle Vm x less the triangle w x^2/2. This relationship may also be stated as Mn = Mm + Vx, where V is the average shear between m and n.
By the area method moments are usually equal to the area of one or more rectangles and/or triangles. It is best to first compute and draw the shear diagram and then compute the moments as the area of the shear diagram.
From the diagrams and derivation we may conclude:
• Positive shear implies increasing bending moment.
• Zero shear (change from + to -) implies peak bending moment (useful to locate maximum bending moment).
• Negative shear implies decreasing bending moment. Even though the forgoing is for uniform load, it applies to concentrated load and non-uniform load as well. The derivation for such loads is similar.