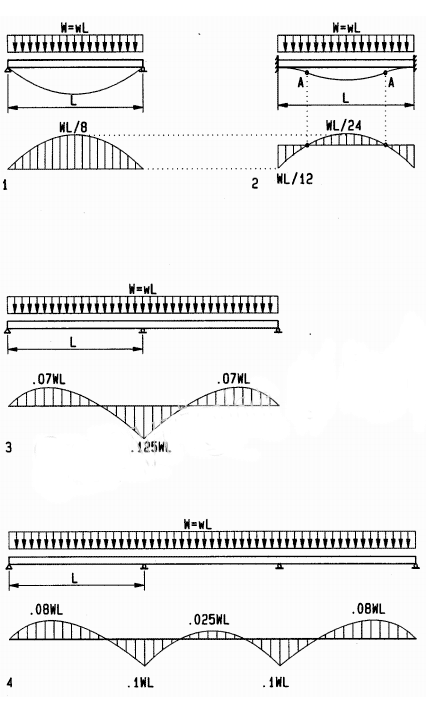
Indeterminate beams include beams with fixed-end (moment resistant) supports and beams of more than two supports, referred to as continuous beams. The design of statically indeterminate beams cannot be done by static equations alone. However, bending coefficients, derived by mechanics, may be used for analysis of typical beams.
The bending moment is computed, multiplying the bending coefficients by the total load W and span L between supports. For continuous beams, the method is limited to beams of equal spans for all bays. The coefficients here assume all bays are loaded.
Coefficients for alternating live load on some bays and combined dead load plus live load on others, which may result in greater bending moments, are in Appendix A. Appendix A also has coefficients for other load conditions, such as various point loads. The equation for bending moments by bending coefficients is:
M = C L W
M = bending moment
C = bending coefficient
L = span between supports
W = w L (total load per bay)
w = uniform load in plf (pounds / linear foot
1 Simple beam
2 Fixed-end beam (combined positive plus negative moments equal the simple-beam moment)
3 Two-span beam
4 Three-span beam
The bending moment is computed, multiplying the bending coefficients by the total load W and span L between supports. For continuous beams, the method is limited to beams of equal spans for all bays. The coefficients here assume all bays are loaded.
Coefficients for alternating live load on some bays and combined dead load plus live load on others, which may result in greater bending moments, are in Appendix A. Appendix A also has coefficients for other load conditions, such as various point loads. The equation for bending moments by bending coefficients is:
M = C L W
M = bending moment
C = bending coefficient
L = span between supports
W = w L (total load per bay)
w = uniform load in plf (pounds / linear foot
1 Simple beam
2 Fixed-end beam (combined positive plus negative moments equal the simple-beam moment)
3 Two-span beam
4 Three-span beam