Graphic vector are powerful means to design funicular structures, like arches and suspension roofs; providing both form and forces under uniform and random loads.
Arch
Assume:
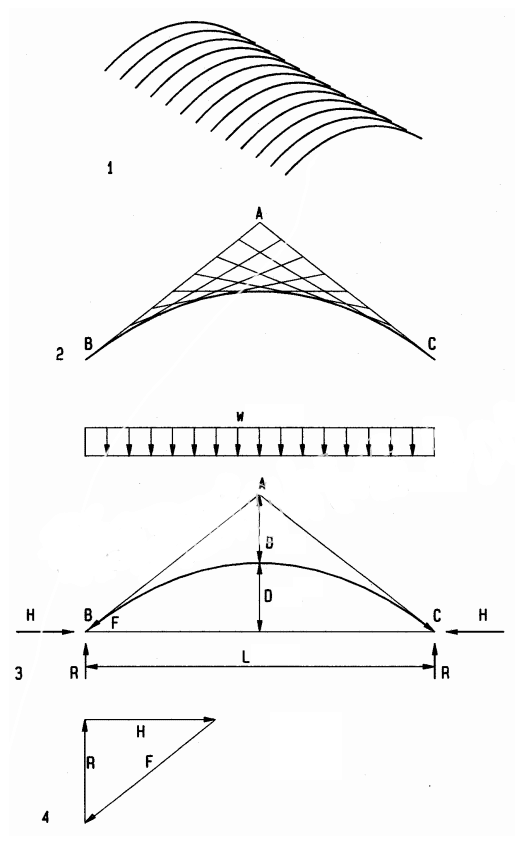
1 Arch structure
2 Parabolic arch by graphic method
Process:
Draw AB and AC (tangents of arch at supports)
Divide tangents AB and AC into equal segments
Lines connecting AB to AC define parabolic arch envelope
3 Arch profile
Process:
Define desired arch rise D (usually D = L/5)
Define point A at 2D above supports
AB and AC are tangents of parabolic arch at supports
Compute vertical reactions R = w L /2
4 Equilibrium vector polygon at supports (force scale: 1” = 50 k) Process:
Draw vertical vector (reaction R)
Complete vector polygon (diagonal vector parallel to tangent)
Measure vectors (H = horizontal reaction, F = max. arch force)
Note:
The arch force varies from minimum at crown (equal to horizontal reaction), gradually increasing with arch slope, to maximum at the supports.
Arch
Assume:
1 Arch structure
2 Parabolic arch by graphic method
Process:
Draw AB and AC (tangents of arch at supports)
Divide tangents AB and AC into equal segments
Lines connecting AB to AC define parabolic arch envelope
3 Arch profile
Process:
Define desired arch rise D (usually D = L/5)
Define point A at 2D above supports
AB and AC are tangents of parabolic arch at supports
Compute vertical reactions R = w L /2
4 Equilibrium vector polygon at supports (force scale: 1” = 50 k) Process:
Draw vertical vector (reaction R)
Complete vector polygon (diagonal vector parallel to tangent)
Measure vectors (H = horizontal reaction, F = max. arch force)
Note:
The arch force varies from minimum at crown (equal to horizontal reaction), gradually increasing with arch slope, to maximum at the supports.