Quantcast
Channel: BUILDER'S ENGINEER
Viewing all 117 articles
Browse latest View live
↧

STRUCTURES - SUSPENSION ROOF

January 13, 2014, 6:47 pm
$
0
0
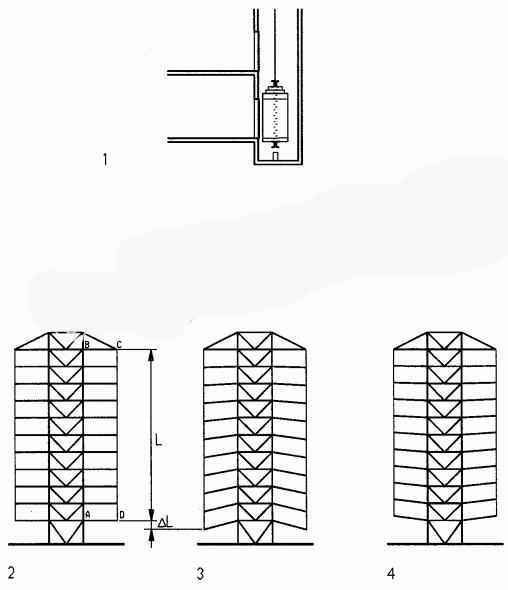
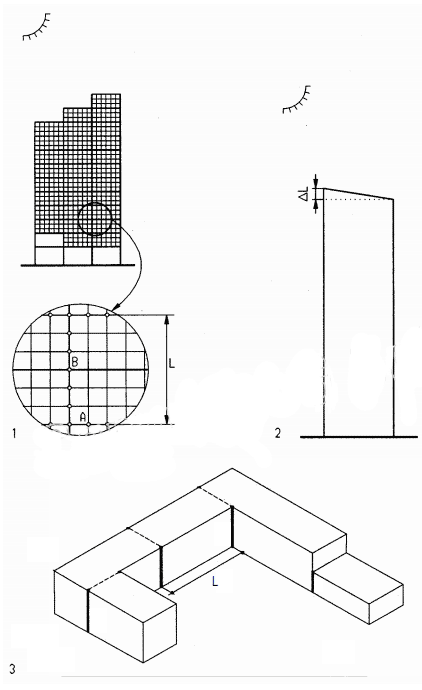
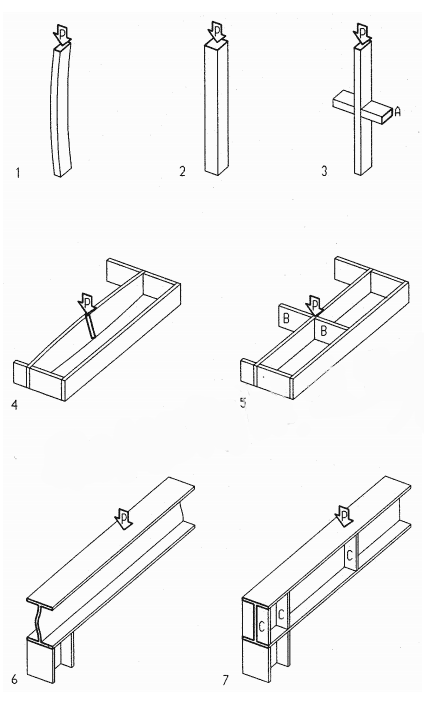
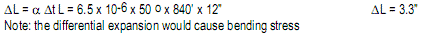Assume:



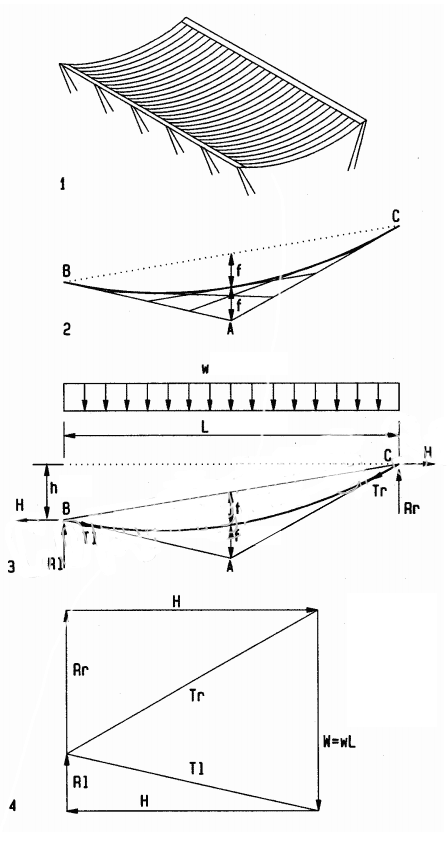
1  Cable roof structure

2  Parabolic cable by graphic method

 Process:
  Draw AB and AC (tangents of cable at supports)
  Divide tangents AB and AC into equal segments
  Lines connecting AB to AC define parabolic cable envelop

3 Cable profile

 Process:
  Define desired cable sag f (usually f = L/10)
  Define point A at 2f below midpoint of line BC
  AB and AC are tangents of parabolic cable at supports
  Compute total load W = w L

4  Equilibrium vector polygon at supports (force scale: 1” = 50 k)
 Process:
  Draw vertical vector (total load W)
  Draw equilibrium polygon W-Tl-Tr
  Draw equilibrium polygons at left support Tl-H-Rl
  Draw equilibrium polygons at right support Tr-Rr-H
  Measure vectors H, Rl, Rr at force scale

Note:  This powerful method finds five unknowns: H, RI, Rr. Tl. Tr The maximum cable force is at the highest support


↧
Search

STRUCTURES - FORCE TYPES

January 22, 2014, 5:29 pm
$
0
0
Forces on structures include tension, compression, shear, bending, and torsion.  Their  effects and notations are tabulated below and all but bending and related shear are  described on the following pages.  Bending and related shear are more complex and further described in the next part.


1  Axial force (tension and compression)
2 Shear
3 Bending
4 Torsion
5 Force actions
6  Symbols and notations

A Tension
B Compression
C Shear
D Bending
E Torsion

STRUCTURES - FORCE TYPES
↧
↧

STRUCTURES: FORCE VS. STRESS

January 29, 2014, 5:51 pm
$
0
0
Force and stress refer to the same phenomena, but with different meanings.  Force is an external action, measured in absolute units: # (pound), k (kip); or SI units: N (Newton),  kN (kilo Newton).  Stress is an internal reaction in relative units (force/area ), measured in psi (pound per square inch), ksi (kip per square  inch); or SI units: Pa (Pascal), kPa (kilo Pascal).  Axial stress is computed as:

f = P / A

where

 f = stress
 P = force
 A = cross section area

Note: stress can be compared to allowable stress of a given material.

Force is the load or action on a member
•  Stress can be compared to allowable stress for any material, expressed as:
 F ≥ f  (Allowable stress must be equal or greater than actual stress)

where

  F = allowable stress
  f = actual stress

The type of stress is usually defined by subscript:

 Fa, fa   (axial stress, capital F = allowable stress)
 Fb, fb   (bending stress, capital F = allowable stress)
 Fv, fv   (shear stress, capital F = allowable stress)

The following examples of axial stress demonstrate force and stress relations:


Note:  The heel would sink into the wood, yield it and mark an indentation

STRUCTURES: FORCE VS. STRESS
↧

STRUCTURES: AXIAL STRESS

February 11, 2014, 9:33 am
$
0
0
Axial stress acts in the axis of members, such as columns.  Axial tension is common in rods and cables; wile axial compression is common in walls and columns.  The following  examples illustrates axial design and analysis.  Analysis determines if an element is ok;  design defines the required size.  The equation, fa = P/A, is used for analysis.  The  equation A = P/Fa, is used for design.  Allowable stress, Fa, includes a factor of safety.

1  Crane cable design 


2  Suspension hanger analysis (Hong Kong-Shanghai bank) 


3 Post/footing analysis 


4  Slab/wall/footing, analyze a 1’ wide strip

STRUCTURES: AXIAL STRESS
↧

STRUCTURES: SHEAR STRESS

February 18, 2014, 5:43 pm
$
0
0
Shear stress occurs in many situations, including the following examples, but also in  conjunction with bending, described in the next chapter on bending.  Shear stress  develops as a resistance to sliding of adjacent parts or fibers, as shown on the following  examples.  Depending on the number of shear planes (the joining surface [A] of connected elements) shear is defined as single shear or double shear.

A Shear plane
B Shear crack


STRUCTURES: SHEAR STRESS

↧
↧

STRUCTURES: TORSION

February 25, 2014, 7:48 pm
$
0
0
Torsion is very common in machines but less common in building structures.  The examples here include a small detail and an entire garage.

1 Door handle 


2 Tuck-under parking


Note: The torsion moment is the product of base shear v and lever arm e, the distance from  center of mass to center of resistance (rear shear wall). In the past, torsion of tuck-under parking was assumed to be resisted by cross shear walls.  However, since the Northridge Earthquake of 1994 where several buildings with tuck-under parking collapsed, such buildings are designed with moment resistant  beam/column joints at the open rear side.

STRUCTURES: TORSION
↧

STRUCTURES - PRINCIPLE STRESS

March 6, 2014, 1:50 pm
$
0
0
Shear stress in one direction, at 45 degrees acts as tensile and compressive stress, defined as principle stress.  Shear stress is zero in the direction of principle stress, where the normal stress is maximum.  At any direction between maximum principle stress and maximum shear stress, there is a combination of shear stress and normal stress.  The magnitude of shear and principle stress is sometimes required for design of details.  Professor Otto Mohr of Dresden University develop 1895 a graphic method to define the  relationships between shear stress and principle stress, named Mohr’s Circle.  Mohr’s circle is derived in books on mechanics (Popov, 1968).



Isostatic lines

Isostatic lines define the directions of principal stress to visualize the stress trajectories in beams and other elements.  Isostatic lines can be defined by experimentally by photo-elastic model simulation or graphically by Mohr’s circle.

1  Simple beam with a square marked for investigation
2  Free-body of square marked on beam with shear stress arrows
3  Free-body square with shear arrows divided into pairs of equal effect
4  Free-body square with principal stress arrows (resultant shear stress vectors)
5  Free-body square rotated 45 degrees in direction of principal stress
6  Beam with isostatic lines (thick compression lines and thin tension lines)

Note:

Under gravity load beam shear increases from zero at mid-span to maximum at supports. Beam compression and tension, caused by bending stress, increase from zero at both supports to maximum at mid-span.  The isostatic lines reflect this stress pattern; vertical orientation dominated by shear at both supports and horizontal orientation dominated by normal stress at mid-span.  Isostaic lines appear as approximate tension “cables” and compression “arches”.

↧

STRUCTURES - STRAIN EXAMPLES

March 11, 2014, 1:11 pm
$
0
0
1 Elevator cables
Assume 
Elongation under load
2 Suspended building
3 Differential strain
Assume

4 Shorten hangers under DL to reduce differential strain, or prestress strands to reduce ∆L by half


Note: Differential strain is additive since both strains are downwards
To limit differential strain, suspended buildings have <= 10 stories / stack

STRUCTURES - STRAIN EXAMPLES
↧
Search

Buildings: Thermal examples

March 19, 2014, 11:32 am
$
0
0
1 Curtain wall
Assume: 

Aluminum curtain wall, find required expansion joint


Thermal strain


2  High-rise building, differential expansion
Assume:

Steel columns exposed to outside temperature


Differential expansion






3  Masonry expansion joints 
(masonry expansion joints should be at maximum L = 100’)
Assume

Buildings: Thermal examples
↧
↧

STABILITY OF STRUCTURES

March 28, 2014, 5:16 pm
$
0
0
Stability is more complex and in some manifestations more difficult to measure than  strength and stiffness but can be broadly defined as capacity to resist:

•  Displacement
•  Overturning 
•  Collapse
•  Buckling

Diagrams 1-3 give a theoretical definition;  all the other diagrams illustrate stability of conceptual structures.

1 Unstable
2 Neutral
3 Stable
4  Weak stability: high center of gravity, narrow base
5  Strong stability: low center of gravity, broad base
6  Unstable post and beam portal
7   Stable moment frame
8  Unstable T-frame with pin joint at base
9  Stable twin T-frames



 
Buckling stability 

Buckling stability is more complex to measure than strength and stiffness and largely based on empirical test data.. This introduction of buckling stability is intended to give only a qualitative intuitive understanding.

Column buckling is defined as function of slenderness and beam buckling as function of  compactness.  A formula for column buckling was first defined in the 18th century by Swiss mathematician Leonhard Euler.  Today column buckling is largely based on empirical tests which confirmed Euler’s theory for slender columns; though short and stubby columns may crush due to lack of compressive strength.

Beam buckling is based on empirical test defined by compactness, a quality similar to column slenderness.

1  Slender column buckles in direction of least dimension
2  Square column resist buckling equally in both directions
3  Blocking resists buckling about least dimension
4  Long and slender wood joist subject to buckling
5  blocking resists buckling of wood joist
6  Web buckling of steel beam
7  Stiffener plates resist web buckling

A  Blocking of wood stud
B  Blocking of wood joist
C  Stiffener plate welded to web
P Load


↧

Structures: Bending Elements

April 3, 2014, 3:20 pm
$
0
0
Bending elements are very common in structures, most notably as beams.  Therefore, the theory of bending is also referred to as beam theory, not only because beams are the most common bending elements but their form is most convenient to derive and describe the theory.  For convenience, similar elements, such as joists and girders, are also considered beams.  Although they are different  in the order or hierarchy of structures,  their bending behavior is similar to that of beams, so is that of other bending elements, such as slabs, etc., shown on the next page. Thus, although the following description applies to the other bending elements, the beam analogy is used for convenience.

Beams are subject to load that acts usually perpendicular to the long axis but is carried in bending along the long axis to vertical supports.  Under gravity load beams are subject to bending moments that shorten the top in compression and elongate the bottom in tension. Most beams are also subject to shear, a sliding force, that acts both horizontally and vertically. Because beams and other bending elements are very common, the beam  theory is important in structural design and analysis.

As for other structural elements, beam investigation may involve analysis or design;  analysis, if a given beam is defined by architectural or other factors; design, if beam dimensions must be determined to support applied loads within allowable stress and deflection. Both, analysis and design, require to find the tributary load, reactions, shear, and bending moment.  In addition, analysis requires to find deflections, shear- and  bending stress, and verify if they meet allowable limits; by contrast design requires sizing  the beam, usually starting with an estimated size.

The following notations are commonly used for bending and shear stress:


Allowable stresses are given in building codes for various materials.

Allowable stresses assumed in this chapter are:


The more complex design and analysis of concrete and masonry will be introduces-later.

↧

Structures: Bending and Shear Stress

April 16, 2014, 4:46 pm
$
0
0
ending and shear stresses in beams relate to bending moment and shear force similar to the way axial stress relates to axial force (f = P/A).  Bending and shear stresses are derived here for a rectangular beam of homogeneous material (beam of constant property).  A general derivation follows later with the Flexure Formula.

1  Simple wood beam with hatched area and square marked for inquiry
2  Shear diagram with hatched area marked for inquiry
3  Bending moment diagram with hatched area marked for inquiry 
4  Partial beam of length x, with stress blocks for bending fb and shear fv, where x is assumed a differential (very small) length

Reactions, found by equilibrium ΣM = 0 (clockwise +)


Shear V, found by vertical equilibrium, ΣV=0 (upward +).


Bending moment M, found by equilibrium ΣM=0 (clockwise +) 


Bending stress fb is derived, referring to 4.  Bending is resisted by the force couple C-T,  with lever arm 2/3 d = distance between centroids of triangular stress blocks.  C=T= fb bd/4, M= C(2d/3) = (fbbd/4)(2d/3) = fbbd^2/6, or  fb= M/(bd^2/6); where bd^2/6 = S= Section Modulus for rectangular beam; thus




 * multiplying by 1000 converts kips to pounds, by 12 converts feet to inches. Shear stress fv is derived, referring to 4.  Bending stress blocks pushing and pulling in opposite directions create horizontal shear stress.  The maximum shear stress is fv=C/bx, where b = width and x = length of resisting shear plane.  Shear at left support is V = R.


↧

STRUCTURES EQUILIBRIUM METHOD

April 23, 2014, 8:24 am
$
0
0
Cantilever beam with point load

Assume a beam of length L = 10 ft, supporting a load P = 2 k.  The beam bending moment and shear force may be computed, like the external reactions, by equations of equilibrium ΣH=0, ΣV= 0, and ΣM=0.  Bending moment and shear force cause bending-and shear stress, similar to axial load yielding axial stress f= P/A.

1      Cantilever beam with concentrated load
V     Shear diagram (shear force at any point along beam)
M    Bending moment diagram (bending moment at any point along beam)
∆     Deflection diagram (exaggerated for clarity) 

Reactions, found by equilibrium, ΣV=0 (up +) and ΣM=0 (clockwise +)


Shear V, found by vertical equilibrium, ΣV=0 (up +)


Left of a and right of b, shear is zero because there is no beam to resist it (reaction at b reduces shear to zero).  Shear may be checked, considering it starts and stops with zero. Concentrated loads or reactions change shear from left to right of them.  Without load between a and b (beam DL assumed negligible) shear is constant.

Bending moment M, found by moment equilibrium, ΣM=0 (clockwise +)


The mid-span moment being half the moment at b implies linear distribution.  The support reaction moment is equal and opposite to the beam moment. 

Deflection ∆ is described later.  Diagrams visualize positive and negative bending by concave and convex curvature, respectively.  They are drawn, visualizing a highly flexible beam, and may be used to verify bending.

STRUCTURES EQUILIBRIUM METHOD
↧
↧

STRUCTURES SIMPLE BEAM WITH UNIFORM LOAD

April 30, 2014, 11:58 am
$
0
0
1  Beam of L= 20 ft span, with uniformly distributed load w = 100 plf
2  Free-body diagram of partial beam x units long
3 Shear diagram
4  Bending moment diagram

To find the distribution of shear and bending along the beam, we investigate the beam at intervals of 5’, from left to right.  This is not normally required. 

Reactions R are half the load on each support due to symmetry 


Shear force Vx at any distance x from left is found using ∑ V = 0 


V  = R - w x


Bending moment Mx at any distance x from left is found by ∑ M = 0. 

∑ M = 0;    R x – w x (x/2) - Mx = 0;   solving for Mx 


Bending is zero at both supports since pins and rollers have no moment resistance. Since the bending formula Mx= Rx-wx2/2 is quadratic, bending increase is quadratic (parabolic curve) toward maximum at center, and decreases to zero at the right support. For simple beams with uniform load the maximum shear force is at the supports and the maximum bending moment at mid-span (x= L/2) are:

Vmax = R = w L / 2 


Mmax = wL^2 / 8

This formula is only for simple beams with uniform load.  Verifying example:



STRUCTURES SIMPLE BEAM WITH UNIFORM LOAD
↧

STRUCTURES - AREA METHOD FOR BEAM DESIGN

May 7, 2014, 9:50 am
$
0
0
The area method for beam design simplifies computation of shear forces and bending moments and is derived, referring to the following diagrams:
1  Load diagram on beam
2 Beam diagram
3 Shear diagram
4 Bending diagram

The area method may be stated:

•  The shear at any point n is equal to the shear at point m plus  the area of the load diagram between m and n. 

•  The bending moment at any point n is equal to the moment at point m plus the area of the shear diagram between m and n.

The shear force is derived using vertical equilibrium:

∑ V = 0;   Vm - w x - Vn = 0;  solving for Vn

Vn = Vm-wx

where w x is the load area between m and n (downward load w = negative).

The bending moment is derived using moment equilibrium: 

∑ M = 0;    Mm + Vmx – w x x/2 - Mn = 0;  solving for Mn


where Vmx – wx^2/2 is the shear area between m and n, namely, the rectangle    Vm x less the triangle w x^2/2.  This relationship may also be stated as Mn = Mm + Vx, where V is the average shear between m and n.

By the area method moments are usually equal to the area of one or more rectangles and/or triangles.  It is best to first compute and draw the shear diagram and then compute the moments as the area of the shear diagram.

From the diagrams and derivation we may conclude:

•  Positive shear implies increasing bending moment. 
•  Zero shear (change from + to -) implies peak bending moment (useful to locate maximum bending moment). 
•  Negative shear implies decreasing bending moment. Even though the forgoing is for uniform load, it applies to concentrated load and non-uniform load as well.  The derivation for such loads is similar.

STRUCTURES - AREA METHOD FOR BEAM DESIGN
↧
Search

STRUCTURES EXAMPLE BEAM DESIGN

May 14, 2014, 12:10 pm
$
0
0
V   Shear diagram.
M  Bending diagram.
∆   Deflection diagram. 
I    Inflection point (change from + to - bending).

Reactions

  R= 400plf (24)/2      R = 4800 lbs

Shear 


Moment


Try 4x10 beam  

Bending stress  

f b = Mmax/S= 5000 (12)/50      f b = 1200 psi
                                                  1200 < 1450, ok

Shear stress  

f v = 1.5V/bd=1.5(2800)/[3.5(9.25)]       f v = 130 psi
                                                               130 > 95, not ok

Try 6x10 beam  
f v = 1.5V/bd=1.5 (2800)/[5.5 (9.25)]      f v= 83 psi
                                                                83 < 95, ok

Note: increased beam width is most effective to reduce shear stress; but increased depth  is most effective to reduce bending stress.

EXAMPLE BEAM DESIGN
↧

STRUCTURES EXAMPLE BEAM ANALYSIS

May 21, 2014, 10:19 am
$
0
0
Reactions


Shear


Find x, where shear = 0 and bending = maximum:

Vbr-w2 x = 0;  x = Vbr/w2 = 2000/200      x = 10 ft

Moment 


Section modulus 

Bending stress

Shear stress
Note: stress is figured, using absolute maximum bending and shear, regardless if positive  or negative.  Lumber sizes are nominal, yet  actual sizes are used for computation.   Actual sizes are ½ in. less for lumber up to 6 in. nominal and ¾ in. less for larger sizes:  4x8 nominal is 3½x7¼ in. actual. 

Note: in the above two beams shear stress is more critical (closer to the allowable stress)  than bending stress, because negative cantilever moments partly reduces positive  moments. 

STRUCTURES EXAMPLE BEAM ANALYSIS
↧
↧

STRUCTURES INDETERMINATE BEAMS

May 27, 2014, 9:48 am
$
0
0
Indeterminate beams include beams with fixed-end (moment resistant) supports and beams of more than two supports, referred to as continuous beams. The design of  statically indeterminate beams cannot be done by static equations alone. However, bending coefficients, derived by mechanics, may be used for analysis of typical beams. 

The bending moment is computed, multiplying the bending coefficients by the total load W and span L between supports.  For continuous beams, the method is limited to beams  of equal spans for all bays.  The coefficients here assume all bays are loaded. 

Coefficients for alternating live load on some bays and combined dead load plus live load  on others, which may result in greater bending moments, are in Appendix A.  Appendix A  also has coefficients for other load conditions, such as various point loads. The equation  for bending moments by bending coefficients is:

M = C L W

M = bending moment
C = bending coefficient
L = span between supports
W = w L (total load per bay)
w = uniform load in plf (pounds / linear foot

1 Simple beam
2  Fixed-end beam (combined positive plus negative moments equal the simple-beam moment)
3 Two-span beam
4 Three-span beam

STRUCTURES INDETERMINATE BEAMS
↧

BEAMS FLEXURE FORMULA

June 4, 2014, 11:56 am
$
0
0
The flexure formula gives the internal bending stress caused by an external moment on a beam or other bending member of homogeneous material.  It is derived here for a rectangular beam but is valid for any shape. 

1  Unloaded beam with hatched square
2  Beam subject to bending with hatched square deformed
3  Stress diagram of deformed beam subject to bending

Referring to the diagram, a beam subject to positive bending assumes a concave curvature (circular under pure bending).  As  illustrated by the hatched square, the top shortens and the bottom elongates, causing compressive stress on the top and tensile stress on the bottom.  Assuming stress varies linearly with strain, stress distribution over the beam depth is proportional to strain deformation.  Thus stress varies linearly over the depth of the beam and is zero at the neutral axis (NA).  The bending stress fy at any  distance y from the neutral axis is found, considering similar triangles, namely fy relates  to y as f relates to c; f is the maximum bending stress at top or bottom and c the distance  from the Neutral Axis, namely fy / y = f / c. Solving for fy yields

fy = y f / c

To satisfy equilibrium, the beam requires an internal resisting moment that is equal and  opposite to the external bending moment.  The internal resisting moment is the sum of all partial forces F rotating around the neutral axis with a lever arm of length y to balance the external moment.  Each partial force F is the productof stress fy and the partial area a on which it acts, F = a fy.  Substituting fy = y f / c, defined above, yields F = a y f / c.  Since the internal resisting moment M is the sum of all forces F times their lever arm y to the  neutral axis, M = F y = (f/c) Σ y y a = (f/c) Σ y^2 a, or M = I f/c, where the term Σy^2 a is defined as  moment of inertia (I =  Σy^2 a) for convenience.  In formal calculus the summation of area  a is replaced by integration of the differential area  da, an infinitely small area:
The internal resisting moment equation M = I f/c solved for stress f yields

which gives the bending stress f at any distance c from the neutral axis.  A simpler form  is used to compute the  maximum fiber stress as derived before.  Assuming c as  maximum fiber distance from the neutral axis yields: 
Both the moment of inertia I and section modulus S define the strength of a cross-section regarding its geometric form.

BEAMS FLEXURE FORMULA
↧

BEAMS SECTION MODULUS

June 10, 2014, 12:03 pm
$
0
0
Rectangular beams of homogeneous material, such as wood, are common in practice. 

The section modulus for such beams is derived here.

1  Stress block in rectangular beam under positive bending.
2  Large stress block and lever-arm of a joist in typical upright position.
3  Small, inefficient, stress block and lever-arm of a joist laid flat. 

Referring to 1, the section modulus for a rectangular beam of homogeneous material may be derived as follows.  The force couple C and T rotate about the neutral axis to provide the internal resisting moment.  C and T act at the center of mass of their  respective triangular stress block at d/3 from the neutral axis.  The magnitude of C and T  is the volume of the upper and lower stress block, respectively. 

C = T = (f/2) (bd/2) = f b d/4.

The internal resisting moment is the sum of C and T times their respective lever arm, d/3, to the neutral axis.  Hence

M = C d/3 + T d/3.  Substituting C = T = f bd/4 yields
M = 2 (f bd/4) d/3 = f bd2/6, or M = f S, 

where S = bd2/6, defined as the section modulus for rectangular beams of homogeneous material.
Solving M = f S for f yields the maximum bending stress as defined before: 

f = M/S

This formula is valid for homogeneous beams of any shape; but the formula S = b(d^2)6 is valid for rectangular beams only.  For other shapes S can be computed as S = I  /c as  defined before for the flexure formula.

Comparing a joist of 2”x12” in upright and flat position as illustrated in 2 and 3 yields an interesting observation:


The upright joist is six times stronger than the flat joist of equal cross-section. This demonstrates the importance of correct orientation of bending members, such as beams  or moment frames.

BEAMS SECTION MODULUS
↧
Viewing all 117 articles
Browse latest View live
Search